Abstract
We explore the baryonic Tully–Fisher relation in the Local Group. Rotationally-supported Local Group galaxies adhere precisely to the relation defined by more distant galaxies. For pressure-supported dwarf galaxies, we determine the scaling factor βc that relates their observed velocity dispersion to the equivalent circular velocity of rotationally-supported galaxies of the same mass such that Vo = βcσ*. For a typical mass-to-light ratio ϒ* = 2 M☉/L☉ in the V band, we find that βc = 2. More generally,  . This provides a common kinematic scale relating pressure and rotationally-supported dwarf galaxies.
. This provides a common kinematic scale relating pressure and rotationally-supported dwarf galaxies.
Export citation and abstract BibTeX RIS
1. Introduction
Galaxies obey distinct kinematic scaling laws. Rotationally-supported galaxies follow the Tully & Fisher (1977) relation that links luminosity with the outer circular velocity Vo
. Pressure-supported systems follow the Faber & Jackson (1976) relation that links luminosity to the stellar-velocity dispersion σ*. Though similar, the Tully–Fisher and Faber–Jackson relations are not identical for a number of reasons. For one, the rotation speed V of a disk and the velocity dispersion σ* of a spheroid are not identical measures. In the ideal case of isotropic orbits in a spherical system, the kinetic energy is split evenly among the three spatial dimensions and the equivalent circular speed of a test particle is 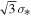 . In a dynamically-cold, rotationally-supported disk with Vo
/σ* ≫ 1, the measured rotation speed is already very close to the circular speed of the gravitational potential, and can be corrected for modest noncircular motions as necessary. On top of this minimal difference between pressure and rotationally-supported systems, the radii at which measurements are made varies widely. The velocity dispersion σ* of bright early-type galaxies is typically measured in their high surface-brightness centers where stars dominate the mass (Cappellari et al. 2007). In rotationally-supported galaxies, the approximately flat circular speed Vo
measured at the outermost radii (e.g., Lelli et al. 2016a) provides the measure that minimizes the scatter in the baryonic Tully–Fisher relation (BTFR; Lelli et al. 2019). This typically occurs in the low-acceleration regime (a < 3700 km2 s−2 kpc−1; Lelli et al. 2017) where dark matter apparently dominates the mass budget. This difference makes it difficult to relate the star-dominated kinematics of the Faber–Jackson relation to those of the BTFR. Nevertheless, there is a relation between σ* and Vo
among early-type galaxies where both quantities can be measured (Serra et al. 2016), so there seems to be a connection.
. In a dynamically-cold, rotationally-supported disk with Vo
/σ* ≫ 1, the measured rotation speed is already very close to the circular speed of the gravitational potential, and can be corrected for modest noncircular motions as necessary. On top of this minimal difference between pressure and rotationally-supported systems, the radii at which measurements are made varies widely. The velocity dispersion σ* of bright early-type galaxies is typically measured in their high surface-brightness centers where stars dominate the mass (Cappellari et al. 2007). In rotationally-supported galaxies, the approximately flat circular speed Vo
measured at the outermost radii (e.g., Lelli et al. 2016a) provides the measure that minimizes the scatter in the baryonic Tully–Fisher relation (BTFR; Lelli et al. 2019). This typically occurs in the low-acceleration regime (a < 3700 km2 s−2 kpc−1; Lelli et al. 2017) where dark matter apparently dominates the mass budget. This difference makes it difficult to relate the star-dominated kinematics of the Faber–Jackson relation to those of the BTFR. Nevertheless, there is a relation between σ* and Vo
among early-type galaxies where both quantities can be measured (Serra et al. 2016), so there seems to be a connection.
In contrast to bright early-type galaxies, the dwarf spheroidals of the Local Group reside predominantly in the low-acceleration regime of dark matter domination. This provides some prospect for relating pressure-supported and rotationally-supported systems on the same characteristic velocity–mass relation. In this paper, we empirically identify the optimal value of βc in Vo = βc σ* that places Local Group dwarf spheroidals on the BTFR. This empirically motivated quantity is analogous to the flat portion 6 of a rotation curve.
We construct the baryonic mass–circular speed relation for Local Group galaxies in Section 2, and check that the BTFR calibrated by external galaxies (Schombert et al. 2020) applies to rotationally-supported galaxies in the Local Group. In Section 3 we identify a sample of dwarf Spheroidals for which we empirically measure the quantity βc . We summarize our results in Section 4.
2. The BTFR in the Local Group
The quantities of luminosity and linewidth traditionally utilized for the Tully–Fisher relation are proxies for more fundamental properties: the baryonic mass Mb = M* + Mg and outer circular speed Vo . The latter quantities define the BTFR (McGaugh 2005). The scatter in the BTFR depends on how these quantities are measured. Empirically, we have found that the scatter is minimized when near-infrared luminosities are utilized to estimate stellar mass (McGaugh & Schombert 2015) and when the outer velocity is measured from extended H i rotation curves. See Lelli et al. (2016a) for the algorithm by which the outer velocity is measured and Lelli et al. (2019) for a comparison to other rotation speed measures.
The BTFR can be written as

as calibrated with 50 galaxies with Cepheid or TRGB distances (Schombert et al. 2020). The dominant uncertainty is not from random errors in the fit but rather from systematics in the stellar-mass estimates and detailed corrections for metallicity and molecular gas (McGaugh et al. 2020). We will determine βc by requiring that dwarfs adhere to Equation (1) in a statistical sense.
The Tully–Fisher relation applies to rotationally-supported galaxies. Prior to determining βc for pressure-supported dwarfs in the Local Group, we first check how the calibration of Schombert et al. (2020) compares with data for those members of the Local Group that have rotating gas disks. This is a useful sanity check since the 50 calibrators of the BTFR are all external to the Local Group.
2.1. Rotationally-supported Local Group Galaxies
Rotationally-supported Local Group galaxies are listed in Table 1 in order of decreasing baryonic mass. These are galaxies with the necessary data (e.g., atomic gas mass, some measure of the outer circular speed). We restrict ourselves to traditional members of the Local Group (Mateo 1998), and do not include other nearby galaxies like those of the outlying NGC 3109 association at D ≃ 1.3 Mpc (see Pawlowski & McGaugh 2014) or more distant (∼2 Mpc) objects like NGC 55, GR 8, IC 5152, and UGCA 438. In particular, NGC 3109 and NGC 55 are in the SPARC sample (Lelli et al. 2016b) and have been used to set our baseline BTFR calibration (Schombert et al. 2020). The galaxies in Table 1 have not been included in the BTFR calibration and are independent of it.
Table 1. Rotationally-supported Local Group Galaxies
| Galaxy | M* | Mg | Vo | References |
|---|---|---|---|---|
| (109 M☉) | (km s−1) | |||
| M31 | 135. | 5.46 | 229.5 ± 2.2 | 1 |
| MW | 60.8 | 12.2 | 197.9 ± 1.9 | 2, 3, 4 |
| M33 | 5.5 | 3.1 | 118.0 ± 1.1 | 5 |
| LMC | 2.0 | 0.60 | 78.9 ± 7.5 | 6, 7, 8 |
| SMC | 0.31 | 0.54 | 56 ± 5 | 6, 7, 9 |
| NGC 6822 | 0.234 | 0.20 | 55 ± 3 | 10 |
| WLM | 0.0163 | 0.077 | 38.7 ± 3.4 | 11, 12 |
| DDO 216 | 0.0152 | 0.00816 | 13.6 ± 5.5 | 11, 12 |
| DDO 210 | 0.00068 | 0.00274 | 16.4 ± 9.5 | 11, 12 |
References. (1) Chemin et al. (2009), (2) Licquia & Newman (2015), (3) Olling & Merrifield (2001), (4) Eilers et al. (2019), (5) Kam et al. (2017), (6) Skibba et al. (2012), (7) Brüns et al. (2005), (8) van der Marel & Sahlmann (2016), (9) Di Teodoro et al. (2019), (10) Weldrake et al. (2003), (11) Zhang et al. (2012), (12) Iorio et al. (2017).
Download table as: ASCIITypeset image
The literature contains many opinions about the relevant quantities for these well-known galaxies. We utilize measurements that are compatible with the data for external galaxies yet independent of our own work. This provides a consistency check on the BTFR calibration of Schombert et al. (2020). We adopt a nominal error of 0.2 dex in mass to reflect the uncertainty in stellar masses stemming from the IMF and the foibles of SED fitting.
2.1.1. Individual Galaxies
Every galaxy is an individual with some peculiarities, so we give a brief description of each.
M31—all the necessary information is provided by Chemin et al. (2009). For the stellar mass, we adopt their stellar population mass estimate as this is most consistent with the stellar population synthesis mass estimates that defines the mass scale of Schombert et al. (2020). Chemin et al. (2009) also discuss other stellar mass estimates that can dip slightly below 1011 M☉, illustrating the dominant systematic uncertainty posed by stellar mass (Bell & de Jong 2001; McGaugh 2005). The rotation speed is measured from H i observations reaching the nearly flat portion of the rotation curve beyond 100'. The rotation curve becomes dodgy beyond 130', so we neglect data beyond this radius which are well beyond the levels reached for the external galaxies to which we compare.
Milky Way—we adopt the stellar population mass estimate of Licquia & Newman (2015). This stellar mass estimate is most comparable to the stellar masses employed to calibrate the BTFR, and is nicely consistent with microlensing constraints on the IMF (Wegg et al. 2017). The adopted stellar mass is heavier than some estimates (Bland-Hawthorn & Gerhard 2016) but lighter than others (Price-Whelan et al. 2021), and is consistent with but independent of our own estimates (McGaugh 2016a, 2019). It is bracketed by kinematic models of the Galactic dark matter halo for which M* can be either a bit higher or a bit lower depending on the choice of halo model (Nesti & Salucci 2013). The gas mass is obtained from integrating the surface-density profile of Olling & Merrifield (2001) scaled to a modern size scale (Gravity Collaboration et al. 2018). For the outer circular speed, we apply the method of Lelli et al. (2016a) to the stellar rotation curve of Eilers et al. (2019). The outer portion of the Milky Way rotation curve declines at the modest but perceptible rate of − 1.7 km s−1 kpc−1, but a larger systematic is caused by the difference in the solar motion found by Eilers et al. (2019) and by McGaugh (2019), with the latter being larger by ∼ 4 km s−1. We do not correct for this difference here to maintain independence. It is small and only worth noting because it exceeds the formal uncertainty, which, as always, should be taken with a grain of salt. This particular difference arises from a difference in the treatment of the term for the gradient of the surface density in the Jeans equation. This difference reconciles an apparent discrepancy between the rotation curve obtained from stars and that from the terminal velocities of interstellar gas (McGaugh 2019).
M33—we adopt the measurements provided by Kam et al. (2017). The stellar mass is based on the same near-infrared scale as our own stellar population estimates. We adjust the mass of atomic and molecular gas to account for helium and metals using the scaling relation of McGaugh et al. (2020). The circular speed is the average over the range 9 < R < 16 kpc where the H i rotation curve is flat. The resulting Vo is somewhat larger than that found by Sanders (1996) and Koch et al. (2018) but slightly smaller than that 7 of López Fune et al. (2017).
LMC—the LMC is clearly interacting with the Milky Way, so one may not expect it to retain equilibrium kinematics. Nevertheless, it falls close to the BTFR (for examples of other perturbed systems; see Verheijen 2001). We adopt the stellar mass estimate of Skibba et al. (2012) as being reasonably comparable to our own stellar mass scale, but smaller (McConnachie 2012) and larger (van der Marel 2006) estimates can be found. The same goes for the gas mass, the boundaries of which are challenging to demarcate given the Magellanic stream. We adopt the gas mass of Brüns et al. (2005), who take care to distinguish between gas in the LMC, SMC, and that in the Magellanic stream. In this and all subsequent cases, we correct the atomic gas mass for the hydrogen mass fraction and molecular gas as described in McGaugh et al. (2020). For the circular speed, we adopt the measurement of van der Marel & Sahlmann (2016) Gaia proper motions.
SMC—the dynamical status of the SMC is even more precarious than that of the LMC, and it shows in published velocity fields. We again adopt the stellar mass estimate of Skibba et al. (2012) and the gas mass of Brüns et al. (2005). For the rotation speed, we adopt the value reported by Di Teodoro et al. (2019) from H i.
NGC 6822—all of the required information is provided by Weldrake et al. (2003). The stellar mass-to-light ratio that they adopt is far from consistent with our own, so we adjust it to a K-band value of ϒ* = 0.63 M☉/L☉ (McGaugh & Schombert 2014).
WLM—data for the dIrr WLM are provided by Iorio et al. (2017) who take their stellar masses from Zhang et al. (2012). This is perhaps the lowest mass Local Group galaxy with a reliable measurement of Vo .
DDO 210, also known as the Aquarius dIrr—all of the required data are provided by Iorio et al. (2017). The kinematics have large uncertainties. The observed H i rotation velocity is extremely small ( ∼ 5 km s−1), comparable to the velocity dispersion of the gas ( ∼ 6 km s−1). This leads to a large uncertainty in the asymmetric drift correction necessary to obtain the circular speed Vo .
DDO 216, also known as the Pegasus Dwarf—data are adopted from Iorio et al. (2017) and are very uncertain. Both DDO 216 and DDO 210 are transitional objects (Mateo 1998) that may be subject to gas stripping: the data may not provide a reliable indicator of the circular speed of their equilibrium gravitational potentials.
There are other dwarf Irregular denizens of the Local Group, but the available kinematic data, if it exists at all, is of even lower quality than that of DDO 216. For example, IC 1613 and Sagittarius DIG do not have reliable estimates of Vo because they are close to face-on. Others have complex H i distributions that are manifestly out of dynamical equilibrium, e.g., IC 10 (Manthey & Oosterloo 2008a, 2008b). For further examples, see Hunter et al. (2012) and Oh et al. (2015). It is challenging to obtain reliable tracers of the equilibrium gravitational potential of very-low-mass galaxies, even those that are very nearby.
2.2. Consistency Check
The data for the Local Group rotators are shown in Figure 1 along with the calibration of Schombert et al. (2020). Agreement between these independent data is satisfactory. Indeed, the galaxies with the most reliable kinematics—M31, the Milky Way, M33, NGC 6822, and WLM—adhere almost perfectly to the relation. It is hard to imagine 8 better agreement.
Figure 1. The baryonic mass–circular velocity relation for Local Group galaxies. Rotationally-supported galaxies with measured Vo (circles, Table 1) are in good agreement with the BTFR calibrated independently with fifty galaxies external to the Local Group (Schombert et al. 2020; solid line; the dashed line is the extrapolation below the lowest mass calibrator). Pressure-supported dwarfs (squares) are plotted with their observed velocity dispersions σ* assuming ϒ* = 2 M☉/L☉. Filled squares are color coded by their proximity to M31 (red) or the Milky Way (orange) or neither (green). Open squares are dwarfs whose velocity dispersions may not be reliable tracers of their equilibrium gravitational potential due to tidal effects (see text).
Download figure:
Standard image High-resolution image3. The Equivalent Circular Velocity
In order to properly compare rotationally and pressure-supported dwarfs, we would like to compare apples with apples. That the circular speed corresponding to an observed velocity dispersion is  relies not only on the assumption of isotropy, but also on an implicit assumption that both quantities are measured at the same radius. This is not expected to be the case. The outer orbital speed Vo
of rotationally-supported galaxies is measured at the largest radii available from interferometric 21 cm observations (Lelli et al. 2016a) that tend to extend beyond the edge of the stellar disk. In contrast, the velocity dispersions of dwarf galaxies in the Local Group are measured from spectra of individual stars. A fair sampling of such tracers would place half of them inside the half-light radius, which is significantly less than the radii probed by Vo
. We therefore do not expect the common assumption of
relies not only on the assumption of isotropy, but also on an implicit assumption that both quantities are measured at the same radius. This is not expected to be the case. The outer orbital speed Vo
of rotationally-supported galaxies is measured at the largest radii available from interferometric 21 cm observations (Lelli et al. 2016a) that tend to extend beyond the edge of the stellar disk. In contrast, the velocity dispersions of dwarf galaxies in the Local Group are measured from spectra of individual stars. A fair sampling of such tracers would place half of them inside the half-light radius, which is significantly less than the radii probed by Vo
. We therefore do not expect the common assumption of 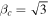 to suffice to make an apples to apples comparison of σ* with Vo
.
to suffice to make an apples to apples comparison of σ* with Vo
.
In practice, both the number of stars observed in each dwarf (which can range from a mere few to thousands) and their locations within each dwarf vary widely from case to case. Sometimes it is possible to obtain detailed velocity dispersion profiles σ*(r) (e.g., Walker et al. 2007), and the considerations here are unnecessary. More commonly, however, one has perhaps a dozen stars that suffice to define a single velocity dispersion at whatever location the observed stars happen to reside. This is taken to be characteristic of the global properties of the system, but the effective radius of such measurements is not equivalent to the outer velocity measured in rotationally-supported galaxies. So in addition to the issue of orbital isotropy, the value of βc also accounts for differences in the effective radius.
One convention is to reference the velocity dispersions of dwarf spheroidals to their half-light radii, σ*(r1/2) (Wolf et al. 2010). This is equivalent to the luminosity-weighted velocity dispersion that one would obtain from the unresolved spectra of more distant galaxies. By calibrating βc locally, we hope to extend its application to future discoveries of dwarfs beyond the Local Group.
Figure 2 shows the rotation curve of the Local Group dIrr WLM (Iorio et al. 2017) and the equivalent circular speed curve for the dwarf spheroidal Leo I. The latter depends on the anisotropy of the orbits, which is generally unknown. One could view anisotropy as a contributor to the uncertainty in the circular speed that grows away from the half-light radius (Wolf et al. 2010; Figure 2). Rather than try to estimate the likely range of anisotropy among dwarfs, we instead choose to ask the data. The outer velocity is related to the measured velocity dispersion; what value of βc reconciles pressure-supported dwarfs with the BTFR?
Figure 2. The rotation curve of the gas rich Local Group dIrr WLM (Iorio et al. 2017, left) and the equivalent circular velocity curve of the pressure-supported dSph Leo I (right). The filled point represents the luminosity-weighted circular speed 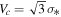 at the 3D half-light radius where variation due to anisotropy is minimized (Wolf et al. 2010). The dotted lines illustrate how the uncertainty grows away from this point due to the compounding effects of anisotropy. The outer circular speed Vo
is marked for both. Note that
at the 3D half-light radius where variation due to anisotropy is minimized (Wolf et al. 2010). The dotted lines illustrate how the uncertainty grows away from this point due to the compounding effects of anisotropy. The outer circular speed Vo
is marked for both. Note that 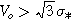 simply because of the shape of the circular velocity curve.
simply because of the shape of the circular velocity curve.
Download figure:
Standard image High-resolution imageThe assumption we make is that galaxies of the same baryonic mass have the same quasiflat outer velocity 9 irrespective of morphology. This is empirically motivated (e.g., Persic et al. 1996), and the obvious assumption to make (e.g., Mo et al. 1998). It is reasonable in any theory. In ΛCDM, dark matter halos of the same mass have the same structure (Navarro et al. 1997). This is what is being probed so long as a galaxy is dark matter dominated. Similarly, a strict relation between velocity and mass is imposed by the force law in MOND (Milgrom 1983) provided that the object is in the low-acceleration regime. Being in the low-acceleration regime is equivalent to being dark matter dominated in the conventional sense. Not all galaxies are dark matter dominated (Persic et al. 1996; McGaugh & de Blok 1998; Starkman et al. 2018), but all of the dwarfs considered here 10 meet the low-acceleration criterion with the exception of the brightest, NGC 205, which is just over the boundary (Lelli et al. 2017).
3.1. Tidal Demarcation
The Local Group dwarfs divide into two families. The brighter dwarfs parallel the Tully–Fisher relation defined by rotationally-supported galaxies (Figure 1). The fainter dwarfs, most of which are the so-called ultrafaints (Simon 2019), break from the relation defined by the bright dwarfs, appearing to have little or no variation in velocity dispersion with luminosity. The velocity dispersions of the ultrafaint dwarfs seem to saturate around σ* ≈ 6 km s−1, albeit with a lot of scatter.
The break that is apparent in Figure 1 was noted by McGaugh & Wolf (2010). They provide a thorough discussion of the many reasons why it might arise. One prominent possibility is tidal effects from the large, nearby hosts, Andromeda, and the Milky Way. Bellazzini et al. (1996) suggested that the quantity 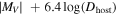 was a good indicator of susceptibility to tidal effects. This and other criteria were considered by McGaugh & Wolf (2010); all yield a similar result. For our purposes here, an effective demarcation between the branches seen in Figure 1 is provided by
was a good indicator of susceptibility to tidal effects. This and other criteria were considered by McGaugh & Wolf (2010); all yield a similar result. For our purposes here, an effective demarcation between the branches seen in Figure 1 is provided by

Note that this is not simply a cut in luminosity, as there is considerable overlap among intermediate luminosity dwarfs depending on the distance from their host. While tidal effects may not be the only reason for the observed break, Equation (2) provides an effective criterion to distinguish between dwarfs that parallel the BTFR and those that do not. It is possible to determine a global value of βc
that reconciles the parallel branch with the BTFR. It is manifestly not possible to find a single value of βc
for those that do not. The reasons why this might occur have been explored in depth by McGaugh & Wolf (2010). These are beyond the scope of this paper; here we simply exclude from further consideration dwarfs with 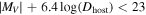 .
.
3.2. Calibrating βc for Local Group Dwarf Spheroidals
To measure the globally optimal value of βc
in Vo
= βc
σ*, we find the median value of βc
that minimizes the difference between the BTFR and the dwarfs selected with the criterion specified by Equation (2). Data for these dwarfs is given in order of decreasing baryonic mass in Table 2. NGC 205 is excluded from the fit as it is not entirely in the low-acceleration regime of dark matter domination. Intriguingly, it is already in good agreement with the BTFR for  , as we might expect if the stars are important to the mass budget.
, as we might expect if the stars are important to the mass budget.
Table 2. Isolated Local Group Dwarfs
| Galaxy |
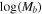
| σ* | βc | Host |
|---|---|---|---|---|
| (106 M☉) | (km s−1) | |||
| NGC 205 | 660. | 35 ± 5 | ... | M31 |
| NGC 185 | 140. | 24 ± 1 | 1.71 ± 0.07 | M31 |
| NGC 147 | 140. | 16 ± 1 | 2.57 ± 0.16 | M31 |
| Fornax | 41. | 11.7 ± 0.9 | 2.59 ± 0.20 | MW |
| And VII | 19. | 13.0 ± 1.0 | 1.93 ± 0.15 | M31 |
| And II | 14. | 9.25 ± 1.1 | 2.51 ± 0.30 | M31 |
| And XXXII | 13. | 8.4 ± 0.6 | 2.73 ± 0.20 | M31 |
| Leo I | 11. | 9.2 ± 0.4 | 2.37 ± 0.10 | MW |
| And XXXI | 8.1 | 10.3 ± 0.9 | 1.97 ± 0.17 | M31 |
| And I | 7.6 | 10.2 ± 1.9 | 1.95 ± 0.36 | M31 |
| Cetus | 5.5 | 8.3 ± 1.0 | 2.21 ± 0.27 | ... |
| And VI | 5.5 |
|
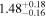
| M31 |
| Sculptor | 4.6 | 9.2 ± 1.1 | 1.91 ± 0.23 | MW |
| And XXIII | 2.0 | 7.1 ± 1.0 | 2.00 ± 0.28 | M31 |
| Pisces | 1.9 |
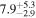
|
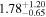
| M31 |
| Leo II | 1.5 | 6.6 ± 0.7 | 2.00 ± 0.21 | MW |
| And XXI | 1.4 |
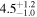
|
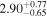
| M31 |
| Tucana | 1.1 |

|

| ... |
| And XV | 0.98 | 4.0 ± 1.4 | 2.98 ± 1.04 | M31 |
| Leo T | 0.74 | 7.5 ± 1.6 | 1.48 ± 0.32 | ... |
| And XVI | 0.68 |

|

| M31 |
| And XXVIII | 0.49 | 4.9 ± 1.6 | 2.05 ± 0.67 | M31 |
| And XXIX | 0.43 | 5.7 ± 1.2 | 1.70 ± 0.36 | M31 |
Note. Mass and βc
assume  .
.
Download table as: ASCIITypeset image
Our procedure averages over any anisotropies present in Local Group dwarfs. It should provide a fair mapping of σ* to Vo provided that there is no systematic alignment of orbital anisotropies in dwarfs along our line of sight (which can happen in some models, e.g., Hammer et al. 2018). Anisotropy in the orbits of stars in Local Group dwarfs is nevertheless an irreducible source of scatter in the BTFR. For this reason alone, we expect more scatter for pressure-supported systems than for rotationally-supported systems.
Further scatter will be caused by variations in the stellar mass-to-light ratio from galaxy to galaxy. In order to perform this exercise, we only need to know the mean stellar mass-to-light ratio for the dwarfs so that we can make an apples to apples comparison with the BTFR (Figure 3). We adopt a nominal V-band ϒ* = 2 M☉/L☉ as a reference point, motivated by the color–magnitude diagrams of resolved stellar populations that suggest ϒ* = 2.4 M☉/L☉ for Sculptor (de Boer et al. 2012a) and 1.7 M☉/L☉ for Fornax (Amorisco & Evans 2012; de Boer et al. 2012b). The resulting value of βc will be degenerate with the choice of ϒ*, so we derive an equation for the covariance that enables the reader to choose whatever mass-to-light ratio seems best.
Figure 3. The baryonic Tully–Fisher relation of Local Group galaxies. Symbols have the same meaning as in Figure 1. For the dwarf spheroidals, we plot Mb
= ϒ*
LV
for ϒ* = 2 M☉/L☉ and Vo
= βc
σ* with βc
= 2. The one exception is the most massive dwarf, NGC 205, for which 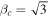 .
.
Download figure:
Standard image High-resolution imageThe value βc that best matches each dSph to the BTFR is given in Table 2. The median βc = 2 for ϒ* = 2 M☉/L☉ in the V band. If instead we use the uncertainty-weighted biweight location, βc = 1.97. This difference is not significant.
The values of βc are plotted in Figure 4, which also shows its covariance with ϒ*. This is given by

Note that the slope of Equation (3) follows from that of the BTFR. One may use this relation for any choice of mass-to-light ratio to find the value of βc that matches the measured velocity dispersions of pressure-supported dwarfs to the circular speeds of rotationally-supported galaxies.
Figure 4. The values of βc that place individual dwarfs precisely on the BTFR. Symbols have the same meaning as in Figure 1. The central value of βc is shown as a point for ϒ* = 2 M☉/L☉; the horizontal dashed line is the median βc = 2. Vertical error bars propagate the uncertainty in the velocity dispersion. Diagonal lines show the covariance with the mass-to-light ratio illustrated by a factor of two variation from ϒ* = 1 (lower left) to ϒ* = 4 M☉/L☉ (upper right). Variation in the stellar mass-to-light ratio from galaxy to galaxy contributes to the scatter, as does anisotropy.
Download figure:
Standard image High-resolution imageIn general, we do not expect the flat portion of the circular velocity curve will be reached by the half-light radius (Figure 2). If it did, we would expect 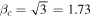 . Instead, we typically expect βc
> 1.73. Treating this as a lower limit implies 〈ϒ*〉 > 1.12 M☉/L☉, which would indeed be rather low for the V-band mass-to-light ratio of an old stellar population.
. Instead, we typically expect βc
> 1.73. Treating this as a lower limit implies 〈ϒ*〉 > 1.12 M☉/L☉, which would indeed be rather low for the V-band mass-to-light ratio of an old stellar population.
One can turn the question around, and attempt to infer variations in the mass-to-light ratios of dwarfs from their location above or below the nominal relation. In doing so, the errors quickly explode due to the strong power-law relation between mass and circular speed. The galaxy that deviates most clearly in this sense is Fornax, which has a low-implied mass-to-light ratio. This is consistent with the observed presence of young stars in Fornax (Battaglia et al. 2006; del Pino et al. 2013; Rusakov et al. 2021) and the mass-to-light ratio inferred from analyses of its color–magnitude diagram (Amorisco & Evans 2012; de Boer et al. 2012b).
The uncertainties are too large in most other cases to make any further inferences about variation in ϒ*. It is worth noting that the velocity dispersions of NGC 147 and NGC 185 (the highest mass galaxies in Figure 4) are clearly different even though they are indistinguishable in luminosity. This might be attributable to differences in the mass-to-light ratio, in their orbital anisotropy, or may simply be an indication of the limits of our method. It is also worth noting that these objects are on rather different orbits around M31 (Sohn et al. 2020), with NGC 147 showing distinct tidal tails while NGC 185 does not (Arias et al. 2016).
Another consideration is the distribution of tracer stars: different stellar populations may have different radial distributions, which affects the term for the logarithmic density gradient in the Jeans equation. Indeed, Laporte et al. (2013) describe how this effect can be used to leverage information about the mass profile of the dark matter halo. Here, we are only making use of a single measured velocity dispersion from whatever tracers were available for observation, in effect averaging over variations in the tracer distribution from galaxy to galaxy. These variations contribute to the scatter in βc , which is modest.
Indeed, there is no clear evidence of much intrinsic scatter in the remainder of the selected dwarf spheroidal data. This statement excludes the ultrafaint dwarfs that were rejected by the tidal criterion of Equation (2), as these clearly do deviate from the Tully–Fisher (Figure 1). While tidal effects may not be the only explanation for the deviance of the ultrafaints (Safarzadeh & Loeb 2021), they seem like the most plausible candidate in the majority of cases (McGaugh & Wolf 2010).
Indeed, the situation for rotationally-supported members of the Local Group (Section 2.1.1) drives home how challenging it can be to obtain robust kinematic probes of the gravitational potentials of low-mass galaxies—even those that are very near to us. It also makes one aware of the importance of tidal interactions: if relatively massive galaxies like the LMC (Besla et al. 2010) and Sgr dwarf (Ibata et al. 1997) are subject to perturbation, what chance is there that ultrafaint dwarfs—many of which are on plunging orbits that take them deep into the Milky Way potential (Simon 2018)—remain unaffected by the same tidal forces?
Finally, we note that in MOND we expect βc = (81/4)1/4 = 2.12 for isotropic orbits in isolated dwarfs in the low-acceleration regime (Milgrom 1995). This corresponds to a mean 〈ϒ*〉 = 2.5 M☉/L☉, which seems plausible as an average mass-to-light ratio for old populations (de Boer et al. 2012a). This is only an approximate test of MOND, as the method employed here neglects the external field effect (e.g., Chae et al. 2020). The criterion imposed by Equation (2) will often but not always succeed in distinguishing dwarfs that should and should not fall on the BTFR (see discussion in McGaugh & Wolf 2010). This is an important distinction in MOND, which is the only theory that has demonstrated the ability to predict velocity dispersions in advance of their observation (McGaugh & Milgrom 2013a, 2013b; Pawlowski & McGaugh 2014; McGaugh 2016b; Famaey et al.2018).
4. Summary
We have investigated the kinematics of pressure-supported and rotationally-supported galaxies in the Local Group. We confirm that rotationally-supported Local Group galaxies are in excellent agreement with the baryonic Tully–Fisher relation calibrated with external galaxies. We further find that the velocity dispersions of pressure-supported dwarf spheroidals can be related to the outer, quasiflat circular speeds of rotationally-supported galaxies through Vo
= βc
σ* with βc
= 2 for ϒ* = 2 M☉/L☉ in the V band. We provide a more general formula for other choices of the stellar mass-to-light ratio (Equation (3)). The median 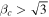 likely indicates that the radius where the circular speed flattens out is greater than the radius were σ* is typically measured. Correlated anisotropy along the line of sight could conceivably have the same effect. Either way, our findings provide a unifying scale with which to discuss systems of differing morphology.
likely indicates that the radius where the circular speed flattens out is greater than the radius were σ* is typically measured. Correlated anisotropy along the line of sight could conceivably have the same effect. Either way, our findings provide a unifying scale with which to discuss systems of differing morphology.
These results are an indication of the tension between galaxy dynamics and cosmologically motivated collisionless dark matter. The quasiflat rotation speed Vo occurs in the low-acceleration regime of dark matter domination, and would seem to be a property of the dark matter halo. This does not sit comfortably with the observational fact that Vo does not depend on the dark matter fraction. It scales strictly with the baryonic mass (Figure 3) irrespective of whether a galaxy is dark matter dominated or not. The baryonic mass and the details of its distribution are far more strongly coupled to the dynamics of galaxies (e.g., Persic et al. 1996; McGaugh 2020) than was anticipated by natural models involving halos of cold dark matter (e.g., McGaugh & de Blok 1998; Mo et al. 1998). More recent, more complicated models do not provide a satisfactory explanation for this simple phenomenology (McGaugh 2021), which remains poorly understood.
We thank the referee for a number of helpful suggestions. S.S.M. thanks Joe Wolf for suggesting that we consider the calculated shapes of the effective circular velocity curves of pressure-supported dwarfs in the same way as the rotation curves of disk galaxies. The work of S.S.M., J.M.S., P.L., and T.V. was supported in part by NASA ADAP grant 80NSSC19k0570 and NSF PHY-1911909. M.S.P. was supported by Leibniz-Junior Research Group grant J94/2020 via the Leibniz Competition, and a Klaus Tschira Boost Fund provided by the Klaus Tschira Stiftung and the German Scholars Organization.
Footnotes
- 6
- 7
López Fune et al. (2017) find V0 = 130.2 ± 1.0 km s−1. This quantity is similar but not identical to our Vo . Their V0 is a parameter of a function (their Equation (18)) that attempts to fit the entire rotation curve while our Vo only quantifies the amplitude of the outer part of the rotation curve (Lelli et al. 2016a). Using the same data (Corbelli et al. 2014), we obtain Vo = 119.6 ± 1.8 km s−1. The difference is entirely a matter of definition; compare the solid and dashed lines in Figure 2 of López Fune et al. (2017).
- 8
This agreement also makes it difficult to imagine a large systematic calibration error in the BTFR determination of H0 = 75.1 ± 2.3 km s−1 Mpc−1 (Schombert et al. 2020).
- 9
See Serra et al. (2016) for a discussion of this point in high-mass early-type galaxies.
- 10
M32 is not considered here as its compact nature makes it star dominated and more akin to giant early-type galaxies.







